Advertisements
Advertisements
प्रश्न
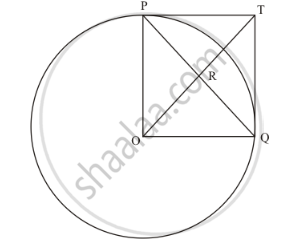
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
उत्तर
In the given figure,
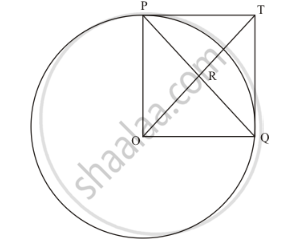
PO = OQ (Since they are the radii of the same circle)
PT = TQ (Length of the tangents from an external point to the circle will be equal)
Now considering the angles of the quadrilateral PTQO, we have,
∠POQ=90° (Given in the problem)
∠OPT=90° (The radius of the circle will be perpendicular to the tangent at the point of contact)
∠TQO=90° (The radius of the circle will be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to 360°. Therefore,
∠POQ+∠TQO+∠OPT+∠PTQ=360°
90°+90°+90°+∠PTQ=360°
∠PTQ=90°
Thus we have found that all angles of the quadrilateral are equal to 90°.
Since all angles of the quadrilateral PTQO are equal to 90° and the adjacent sides are equal, this quadrilateral is a square.
We know that in a square, the diagonals will bisect each other at right angles.
Therefore, PQ and OT bisect each other at right angles.
Thus we have proved.
APPEARS IN
संबंधित प्रश्न
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

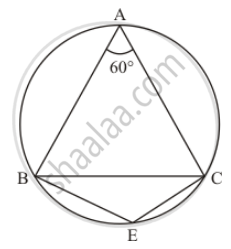
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

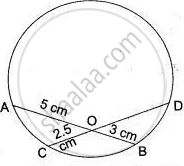
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Can the length of a chord of a circle be greater than its diameter ? Explain.
The longest chord of a circle is __________
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
Is every chord of a circle also a diameter?
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
