Advertisements
Advertisements
प्रश्न
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
उत्तर
Given
O is center of circle
BCD is tangent.
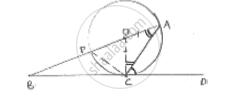
Required to prove: ∠BAC + ∠ACD = 90°
Proof: OA = OC [radius]
In ΔOAC, angles opposite to equal sides are equal.
∠OAC = ∠OCA …. (i)
∠OCD = 90° [tangent is radius are perpendicular at point of contact]
∠ACD + ∠OCA = 90°
∠ACD + ∠OAC = 90° [∵ ∠OAC = ∠BAC]
∠ACD + ∠BAC = 90° ⟶ Hence proved
APPEARS IN
संबंधित प्रश्न
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
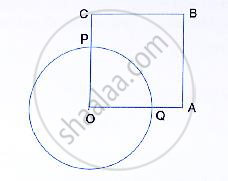
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
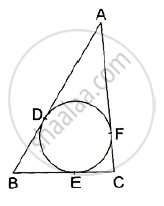
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

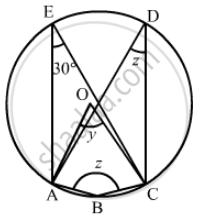
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

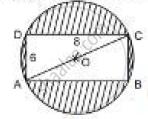
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
The ratio between the circumference and diameter of any circle is _______
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
From the figure, identify a point in the exterior.

