Advertisements
Advertisements
प्रश्न
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
उत्तर
Given ΔABC is isosceles AB = AC
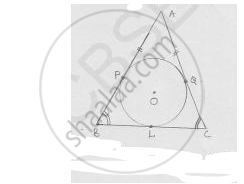
We know that
The tangents from external point to circle are equal in length
From point A, AP = AQ
But AB = AC ⇒ AP + PB = AQ + QC
⇒ PB = PC …. (i)
From B, PB = BL; ….(ii) from C, CL = CQ …..(iii)
From (i), (ii) & (iii)
BL = CL
∴ L bisects BC.
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
Prove that two different circles cannot intersect each other at more than two points.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
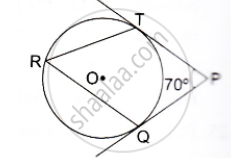
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
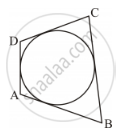
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
