Advertisements
Advertisements
рдкреНрд░рд╢реНрди
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
рдЙрддреНрддрд░
Consider a circle with center O and radius OA = 8cm = r, AB = 15 cm.
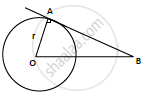
(AB) tangent is drawn at A (point of contact)
At point of contact, we know that radius and tangent are perpendicular.
In ΔOAB, ∠OAB = 90°, By Pythagoras theorem
ЁЭСВЁЭР╡2 = ЁЭСВЁЭР┤2 + ЁЭР┤ЁЭР╡2
`OB = sqrt(8^2 + 15^2)`
`=sqrt(64+225)`
`= sqrt(289)`
= 17 cm
∴ ЁЭСВЁЭР╡ = 17 ЁЭСРЁЭСЪ
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
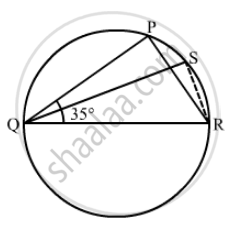
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
In the given figure, if ∠ABC = 45°, then ∠AOC =
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
If the radius of a circle is 5 cm, what will its diameter be?
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?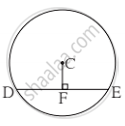
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]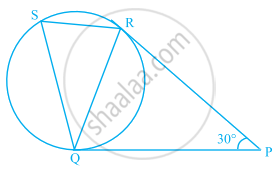
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Say true or false:
Two diameters of a circle will necessarily intersect.
