Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
рдЙрддреНрддрд░
Given,
PQ = 24 cm
OQ = 25 cm
OP = radius = ?
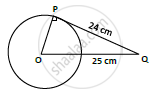
P is point of contact, At point of contact, tangent and radius are perpendicular to each other
∴ ΔPOQ is right angled triangle ∠OPQ = 90°
By Pythagoras theorem,
ЁЭСГЁЭСД2 + ЁЭСВЁЭСГ2 = ЁЭСВЁЭСД2
⇒ 242 + ЁЭСВЁЭСГ2 = 252
⇒`PO = sqrt((25)^2 − (24)^2) = sqrt(625 − 576)`
= `sqrt(49)` = 7ЁЭСРЁЭСЪ
∴ ЁЭСВЁЭСГ = ЁЭСЯЁЭСОЁЭССЁЭСЦЁЭСвЁЭСа = 7ЁЭСРЁЭСЪ
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
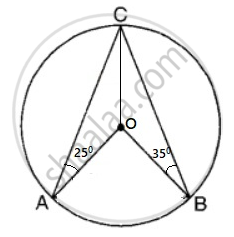
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
