Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
рдЙрддреНрддрд░
OT = radius = 8cm
OP = 17cm
PT = length of tangent = ?
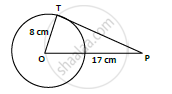
T is point of contact. We know that at point of contact tangent and radius are perpendicular.
∴ OTP is right angled triangle ∠OTP = 90°, from Pythagoras theorem ЁЭСВЁЭСЗ2 + ЁЭСГЁЭСЗ2 = ЁЭСВЁЭСГ2
82 + ЁЭСГЁЭСЗ2 = 172
`PT sqrt(17^2 − 8^2) = sqrt(289 − 64)`
=`sqrt(225)` = 15ЁЭСРЁЭСЪ
∴ PT = length of tangent = 15 cm.
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
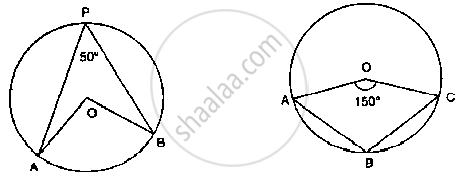
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
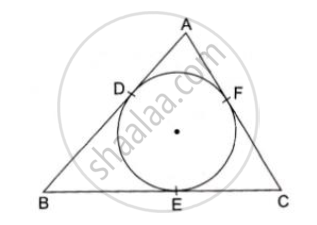
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.
Find the area of a circle of radius 7 cm.
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
From the figure, identify a chord.
