Advertisements
Advertisements
प्रश्न
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
उत्तर
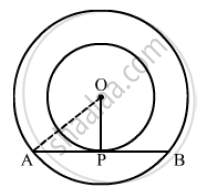
We know that the radius and tangent are perpendicular at their point of contact In right triangle AOP
`AO^2 = OP^2 + PA^2`
⇒ `(6.5) ^2 = (2.5)^2 +PA^2`
⇒`PA^2 = 36`
⇒PA = 6cm
Since, the perpendicular drawn from the center bisects the chord.
∴ PA = PB = 6cm
Now , AB = AP + PB = 6+6 = 12cm
Hence, the length of the chord of the larger circle is 12cm.
APPEARS IN
संबंधित प्रश्न
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure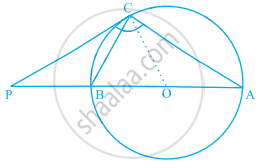
In the given figure, O is the centre of the circle. Name all chords of the circle.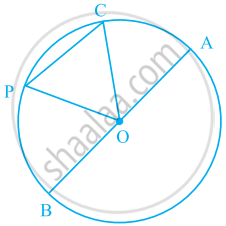
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.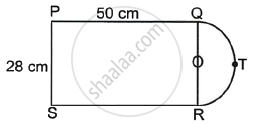
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
