Advertisements
Advertisements
Question
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution
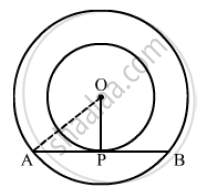
We know that the radius and tangent are perpendicular at their point of contact In right triangle AOP
`AO^2 = OP^2 + PA^2`
⇒ `(6.5) ^2 = (2.5)^2 +PA^2`
⇒`PA^2 = 36`
⇒PA = 6cm
Since, the perpendicular drawn from the center bisects the chord.
∴ PA = PB = 6cm
Now , AB = AP + PB = 6+6 = 12cm
Hence, the length of the chord of the larger circle is 12cm.
APPEARS IN
RELATED QUESTIONS
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
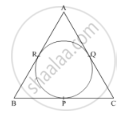
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
From the figure, identify a diameter.
From the figure, identify a segment.

