Advertisements
Advertisements
Question
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

Solution

Given: AB and CD are common tangents to both the circles.
To prove: AB = CD
Proof:
We know that two tangents drawn to a circle for the same exterior point are
equal.
Thus we get
AE = EC (i)
Similarly
ED = EB (ii)
AB = AE + EB (iii)
and
CD = CE + ED (iv)
AB = EC + EB from (i) and (iii)
CD = EC + EB from (ii) and (iv)
Therefore AB = CD
Hence proved.
APPEARS IN
RELATED QUESTIONS
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

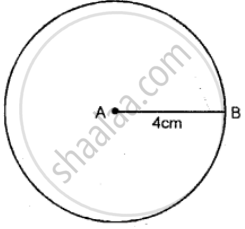
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.