Advertisements
Advertisements
Question
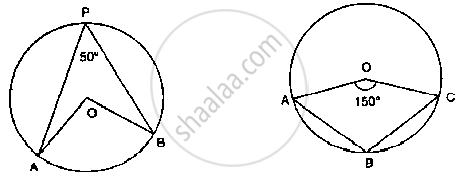
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

Options
A. 55°
B. 70°
C. 45°
D. 35°
Solution
In ΔOPQ:
OP = OQ (Radii of same circle)
⇒ ∠OQP = ∠OPQ (Equal sides have equal angles opposite to them)
∠POQ + ∠OPQ + ∠OQP = 180° (Angle sum property of triangles)
⇒ 70° + 2∠OPQ = 180°
⇒ 2∠OPQ = 180° − 70° = 110°
⇒ ∠OPQ = 55°
It is known that the tangent is perpendicular to the radius through the point of contact.
∴ ∠OPT = 90°
⇒ ∠OPQ + ∠TPQ = 90°
⇒ 55° + ∠TPQ = 90°
⇒ ∠TPQ = 90° − 55° = 35°
The correct answer is D.
APPEARS IN
RELATED QUESTIONS
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.