Advertisements
Advertisements
Question
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
Solution
BC = 6cm AB = 8cm
As ABC is right angled triangle
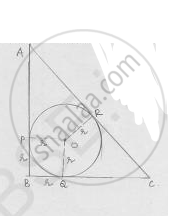
By Pythagoras theorem
𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2 = 62 + 82 = 100
𝐴𝐶 = 10 𝑐𝑚
Consider BQOP ∠B = 90°,
∠BPO = ∠OQB = 90° [At point of contact, radius is perpendicular to tangent]
All the angles = 90° & adjacent sides are equal
∴ BQOP is square BP = BQ = r
We know that
The tangents drawn from any external point are equal in length.
AP = AR = AB – PB = 8 – r
QC = RC = BC – BQ = 6 – r
AC = AR + RC ⇒ 10 = 8 – r + 6 – r
⇒ 10 = 14 – 2r
⇒ 2r = 4
⇒ Radius = 2cm
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
Draw circle with the radii given below.
4 cm
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
