Advertisements
Advertisements
Question
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
Solution
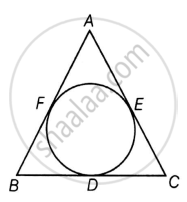
A triangle ABC with BC = a, CA = b and AB = c.
Also, a circle is inscribed, which touches the sides BC, CA and AB at D, E and F, respectively and s is semi-perimeter of the triangle
To Prove: BD = s – b
Proof:
We have,
Semi Perimeter = s
Perimeter = 2s
2s = AB + BC + AC ...[1]
As we know,
Tangents drawn from an external point to a circle are equal
So we have
AF = AE ...[2] [Tangents from point A]
BF = BD ...[3] [Tangents from point B]
CD = CE ...[4] [Tangents from point C]
Adding [2] [3] and [4]
AF + BF + CD = AE + BD + CE
AB + CD = AC + BD
Adding BD both side
AB + CD + BD = AC + BD + BD
AB + BC – AC = 2BD
AB + BC + AC – AC – AC = 2BD
2s – 2AC = 2BD ...[From 1]
2BD = 2s – 2b ...[As AC = b]
BD = s – b
Hence proved.
APPEARS IN
RELATED QUESTIONS
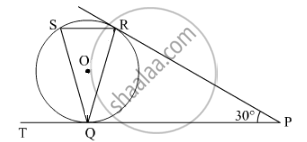
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In the given figure, O is the centre of the circle. Find ∠CBD.

Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?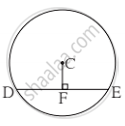
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
