Advertisements
Advertisements
Questions
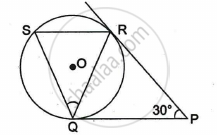
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
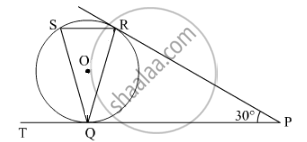
In the given figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the measure of ∠RQS.
Solution
It is given that, ∠RPQ = 30° and PQ and PR are tangents drawn to a circle from P to the same circle.
∴ PQ = PR ...(Tangents drawn from an external point to a circle are equal in length.)
In ∆PQR,
PQ = PR
∴ ∠PQR = ∠PRQ ...(Angles opposite to equal sides are equal.)
Now, In ∆PQR,
∠PQR + ∠PRQ + ∠RPQ = 180° ...(Angle sum property of a triangle)
∴ ∠PQR + ∠PQR + 30° = 180°
∴ 2∠PQR + 30° = 180°
∴ 2∠PQR = 180° − 30°
∴ 2∠PQR = 150°
∴ ∠PQR = 75°
So, ∠PQR = ∠QRS = 75° ...(Alternate angles)
∠PQR = ∠QSR = 75° ...(Alternate segment angles are equal)
and ∠QRS = ∠QSR = 75°
∴ ΔQRS is also an isosceles triangle.
∴ ∠QRS + ∠QSR + ∠RQS = 180°
∴ 75° + 75° + ∠RQS = 180°
∴ ∠RQS = 180° − 150°
∴ ∠RQS = 30°
APPEARS IN
RELATED QUESTIONS
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
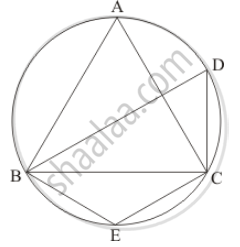
In the given figure, if ∠ABC = 45°, then ∠AOC =
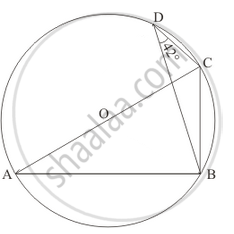
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

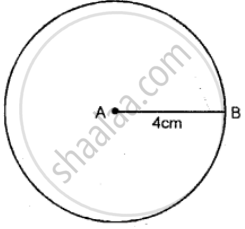
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
From the figure, identify the centre of the circle.