Advertisements
Advertisements
Question
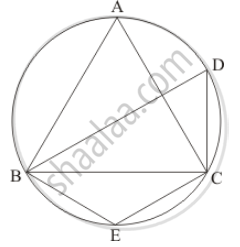
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
Solution
It is given that, ABC is an equilateral triangle
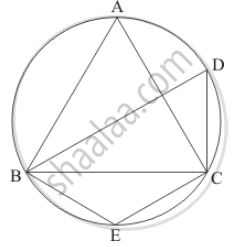
We have to find `angleBDC` and `angleBEC`
Since ΔABC is an equilateral triangle
So, `angleA = angleB = angleC = 60°`
And ABEC is cyclic quadrilateral
So `angle A + angle E = 180°` (Sum of opposite pair of angles of a cyclic quadrilateral is 180°.)
Then,
`angle E = 180° - 60°`
= 120°
Similarly BECD is also cyclic quadrilateral
So,
`angle E + angle D = 180°`
`angleD = 180° - 120°`
= 60°
Hence, `angle BDC `= 60° and `angle BEC = 120°`.
APPEARS IN
RELATED QUESTIONS
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
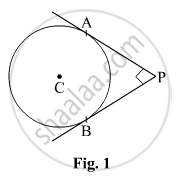
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Use the figure given below to fill in the blank:
Diameter = 2 x ________

A line segment which joins any two points on a circle is a ___________
A line segment joining any point on the circle to its center is called the _____________ of the circle
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
