Advertisements
Advertisements
Question
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
Solution
Given: ΔABC is inscribed in a circle. Bisector of ∠A and perpendicular bisector of BC intersect at point Q.
To prove: A, B, Q and C are con-cyclic.
Construction: Join BQ and QC.
Proof: We have assumed that, Q lies outside the circle.
In ΔBMQ and ΔCMQ,
BM = CM ...[QM is the perpendicular bisector of BC]
∠BMQ = ∠CMQ ...[Each 90°]
MQ = MQ ...[Common side]
∴ ΔBMQ ≅ ΔCMQ ...[By SAS congruence rule]
∴ BQ = CQ [By CPCT] ...(i)
Also, ∠BAQ = ∠CAQ [Given] ...(ii)
From equations (i) and (ii),
We can say that Q lies on the circle ...[Equal chords of a circle subtend equal angles at the circumference]
Hence, A, B, Q and C are con-cyclic.
Hence proved.
APPEARS IN
RELATED QUESTIONS
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
ture or false v
The degree measure of a semi-circle is 180°.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
The length of tangent from an external point on a circle is always greater than the radius of the circle.
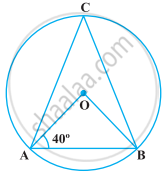
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
