Advertisements
Advertisements
Question
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
Solution
Given: ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawn that it intersect AD at P and BC at Q.
To prove: Points P, Q, C and D are con-cyclic.
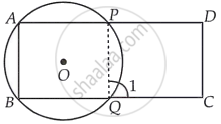
Construction: Join PQ
Proof: ∠1 = ∠A ...[Exterior angle property of cyclic quadrilateral]
But ∠A = ∠C ...[Opposite angles of a parallelogram]
∴ ∠1 = ∠C ...(i)
But ∠C + ∠D = 180° ...[Sum of cointerior angles on same side is 180°]
⇒ ∠1 + ∠D = 180° ...[From equation (i)]
Thus, the quadrilateral QCDP is cyclic.
So, the points P, Q, C and D are con-cyclic.
Hence proved.
APPEARS IN
RELATED QUESTIONS
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
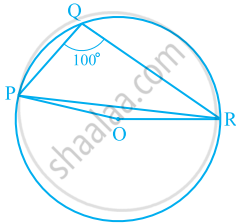
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
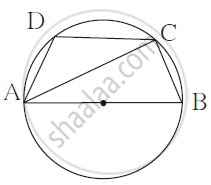
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
