Advertisements
Advertisements
Question
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
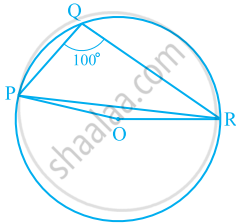
Solution

Consider PR as a chord of the circle.
Take any point S on the major arc of the circle.
PQRS is a cyclic quadrilateral.
∠PQR + ∠PSR = 180° ...(Opposite angles of a cyclic quadrilateral)
⇒ ∠PSR = 180° − 100° = 80°
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
∴ ∠POR = 2∠PSR = 2(80°) = 160°
In ΔPOR,
OP = OR ...(Radii of the same circle)
∴ ∠OPR = ∠ORP ...(Angles opposite to equal sides of a triangle)
∠OPR + ∠ORP + ∠POR = 180° ...(Angle sum property of a triangle)
2∠OPR + 160° = 180°
2∠OPR = 180° − 160° = 20°
∠OPR = 10°
APPEARS IN
RELATED QUESTIONS
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
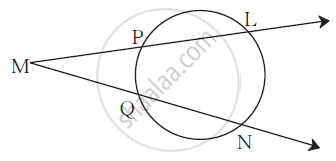
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
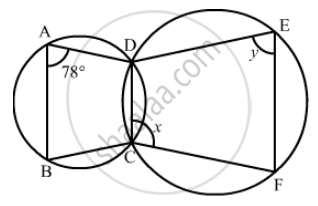
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
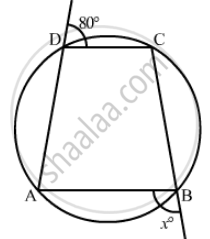
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
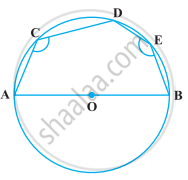
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.