Advertisements
Advertisements
Question
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
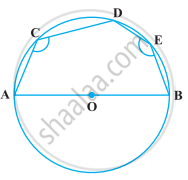
Solution
Since, A, C, D and E are four point on a circle, then ACDE is a cyclic quadrilateral.
∠ACD + ∠AED = 180° ...(i) [Sum of opposite angles in a cyclic quadrilateral is 180°]
Now, ∠AEB = 90° ...(ii)
We know that, diameter subtends a right angle to the circle.
On adding equations (i) and (ii), we get
(∠ACD + ∠AED) + ∠AEB = 180° + 90° = 270°
⇒ ∠ACD + ∠BED = 270°
APPEARS IN
RELATED QUESTIONS
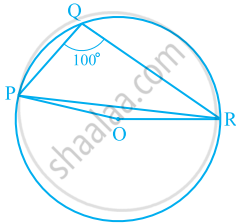
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
