Advertisements
Advertisements
Question
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
Solution
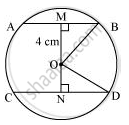
Let AB and CD be two parallel chords in a circle centered at O. Join OB and OD.
Distance of smaller chord AB from the centre of the circle = 4 cm
OM = 4 cm
MB = AB/2 = 6/2 = 3cm
In ΔOMB,
OM2 + MB2 = OB2
(4)2 + (3)2 = OB2
16 + 9 = OB2
OB2 = 25
`OB = sqrt25`
OB = 5cm
In ΔOND,
OD = OB = 5cm (Radii of the same circle)
ND = CD/2 = 8/2 = 4cm
ON2 + ND2 = OD2
ON2 + (4)2 = (5)2
ON2 = 25 - 16 = 9
ON = 3
Therefore, the distance of the bigger chord from the centre is 3 cm.
APPEARS IN
RELATED QUESTIONS
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
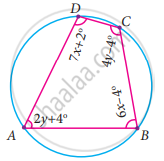
Find all the angles of the given cyclic quadrilateral ABCD in the figure.