Advertisements
Advertisements
Question
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
Solution
Here, ABCD is a rhombus; we have to prove the four circles described on the four sides of any rhombusABCD pass through the point of intersection of its diagonals AC and BD.
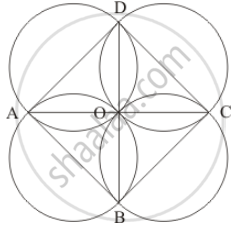
Let the diagonals AC and BD intersect at O.
We know that the diagonals of a rhombus intersect at right angle.
Therefore,
`angle AOB = `90°
`angleBOC = `90°
`angle COD ` = 90°
`angle AOD ` = 90°
Now, `angle AOB ` = 90 means that circle described on AB as diameter passes through O.
Similarly the remaining three circles with BC, CD and AD as their diameter will also pass through O.
Hence, all the circles with described on the four sides of any rhombus ABCD pass through the point of intersection of its diagonals AC and BD.
APPEARS IN
RELATED QUESTIONS
Prove that a cyclic parallelogram is a rectangle.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
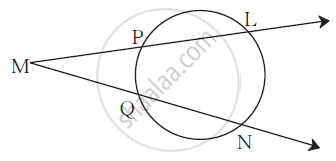
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
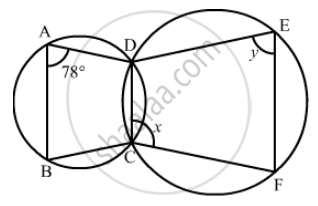
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

Find all the angles of the given cyclic quadrilateral ABCD in the figure.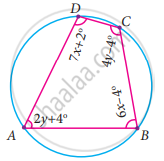
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
