Advertisements
Advertisements
Question
Prove that a cyclic parallelogram is a rectangle.
Solution
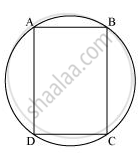
Let ABCD be a cyclic parallelogram.
∠A + ∠C = 180° (Opposite angles of a cyclic quadrilateral) ...(1)
We know that opposite angles of a parallelogram are equal.
∴ ∠A = ∠C and ∠B = ∠D
From equation (1),
∠A + ∠C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2 ∠A = 180°
⇒ ∠A = 90°
Parallelogram ABCD has one of its interior angles, which is 90°. Therefore, it is a rectangle.
APPEARS IN
RELATED QUESTIONS
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
