Advertisements
Advertisements
प्रश्न
Prove that a cyclic parallelogram is a rectangle.
Advertisements
उत्तर
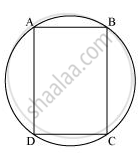
Let ABCD be a cyclic parallelogram.
∠A + ∠C = 180° (Opposite angles of a cyclic quadrilateral) ...(1)
We know that opposite angles of a parallelogram are equal.
∴ ∠A = ∠C and ∠B = ∠D
From equation (1),
∠A + ∠C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2 ∠A = 180°
⇒ ∠A = 90°
Parallelogram ABCD has one of its interior angles, which is 90°. Therefore, it is a rectangle.
APPEARS IN
संबंधित प्रश्न
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
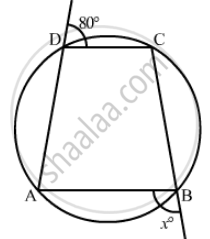
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
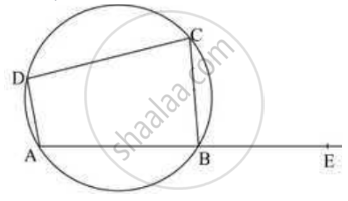
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
