Advertisements
Advertisements
प्रश्न
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
उत्तर
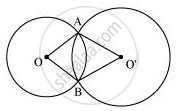
Let two circles having their centres as O and O' intersect each other at point A and B respectively. Let us join OO'.
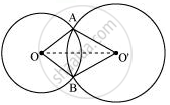
In ΔAOO' and BOO',
OA = OB (Radius of circle 1)
O'A = O'B (Radius of circle 2)
OO' = OO' (Common)
ΔAOO' ≅ ΔBOO' (By SSS congruence rule)
∠OAO' = ∠OBO' (By CPCT)
Therefore, line of centres of two intersecting circles subtends equal angles at the two points of intersection.
APPEARS IN
संबंधित प्रश्न
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
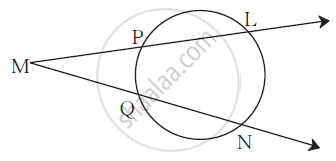
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
