Advertisements
Advertisements
प्रश्न
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
उत्तर
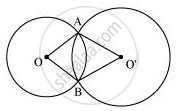
Let two circles having their centres as O and O' intersect each other at point A and B respectively. Let us join OO'.
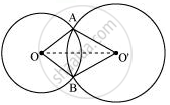
In ΔAOO' and BOO',
OA = OB (Radius of circle 1)
O'A = O'B (Radius of circle 2)
OO' = OO' (Common)
ΔAOO' ≅ ΔBOO' (By SSS congruence rule)
∠OAO' = ∠OBO' (By CPCT)
Therefore, line of centres of two intersecting circles subtends equal angles at the two points of intersection.
APPEARS IN
संबंधित प्रश्न
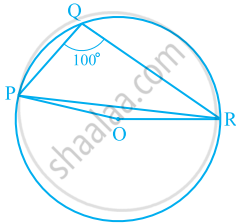
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
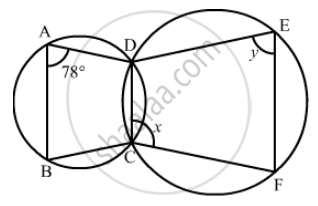
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
