Advertisements
Advertisements
प्रश्न
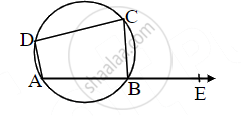
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
उत्तर
m(arc ABC) = 230° .....(i) [Given]
∴ m(arc ADC) + m(arc ABC) = 360° .......[Degree measure of a circle is 360°]
∴ m(arc ADC) = 360° – m(arc ABC)
∴ m(arc ADC) = 360° – 230° .......[From (i)]
∴ m(arc ADC) = 130°
∠ABC = `1/2` m (arc ADC) ......[Inscribed angle theorem]
= `1/2 xx 130^circ`
= 65°
Now, ∠CDA = `1/2` m (arc ABC) ......[Inscribed angle theorem]
∴ ∠CDA = `1/2 xx 230^circ`
∴ ∠CDA = 115° ......(ii)
∠CBE = ∠CDA ......(iiii) [The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle]
∴ ∠CBE = 115° .....[From (ii) and (iii)]
∴ ∠ABC = 65°, ∠CDA = 115°, ∠CBE = 115°.
संबंधित प्रश्न
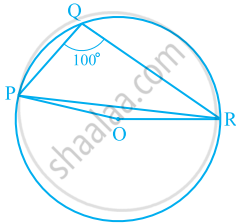
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Prove that a cyclic parallelogram is a rectangle.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

Find all the angles of the given cyclic quadrilateral ABCD in the figure.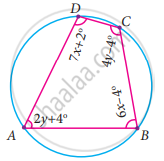
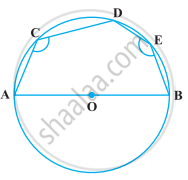
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
