Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
उत्तर
If ABCD is a cyclic quadrilateral in which AB and CD when produced meet in E such that EA = ED, then we have to prove the following, AD || BC
It is given that EA = ED, so
Since, ABCD is cyclic quadrilateral
`x + angleABC = 180 ⇒ angleDAB = 180 - x`
And ; ` x + angleBCD = 180 ⇒ angle BCD = 180- x `
Now,
`angle DAB + angle ABC = x + 180 - x = 180`
Therefore, the adjacent angles `angleDAB ` and `angleABC` are supplementary
Hence, AD || BC
APPEARS IN
संबंधित प्रश्न
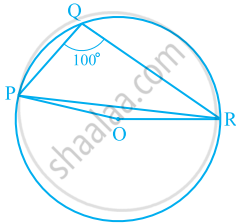
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
