Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
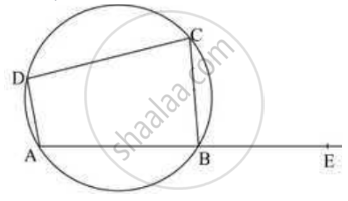
उत्तर

M(arc ABC) = 230°
M(arc ADC) = 360° - M(arc ABC) … complete circle is 360°
M(arc ADC) = 360° - 230° = 130°
∴ ∠AOC = 130°
The angle subtended by an arc at the point on a circle is equal to half of the angle subtended by the same arc at the center
Here arc ADC subtends ∠AOC at center and ∠ABC on a circle
∴ ∠ABC = (1/2) × ∠AOC
= 1/2 × 130°
= 65°
∴ ∠ABC = 65°
∠ABC + ∠CBE = 180° …linear pair of angles
∴ 65° + ∠CBE = 180°
∴ ∠CBE = 180° - 65° = 115°
∴ ∠CBE = 115°
∠CDA + ∠ABC = 180° …opposite pair of cyclic quadrilateral ABCD
∴ ∠CDA + 65° = 180°
∴ ∠CDA = 180° - 65° = 115°
∴ ∠CDA = 115°
Hence ∠ABC = 65°, ∠CDA = 115° and ∠CBE = 115°
APPEARS IN
संबंधित प्रश्न
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
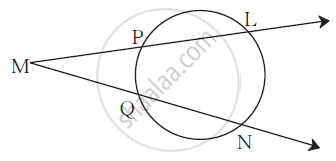
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.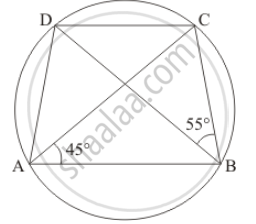
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
