Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
उत्तर
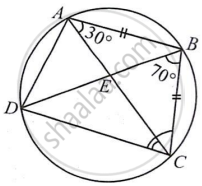
For chord CD,
∠CBD = ∠CAD ...(Angles in the same segment)
∠CAD = 70°
∠BAD = ∠BAC + ∠CAD = 30° + 70° = 100°
∠BCD + ∠BAD = 180° ...(Opposite angles of a cyclic quadrilateral)
∠BCD + 100° = 180°
∠BCD = 80°
In ΔABC,
AB = BC ...(Given)
∴ ∠BCA = ∠CAB ...(Angles opposite to equal sides of a triangle)
⇒ ∠BCA = 30°
We have, ∠BCD = 80°
⇒ ∠BCA + ∠ACD = 80°
30° + ∠ACD = 80°
⇒ ∠ACD = 50°
⇒ ∠ECD = 50°
APPEARS IN
संबंधित प्रश्न
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
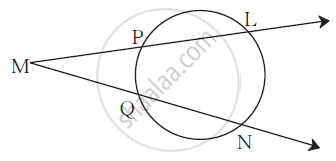
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.