Advertisements
Advertisements
प्रश्न
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
उत्तर

Let ABCD be a cyclic quadrilateral having diagonals BD and AC, intersecting each other at point O.
∠BAD = `1/2angleBOD`
= `180^@/2`
= 90° ...(Consider BD as a chord)
∠BCD + ∠BAD = 180° ...(Cyclic quadrilateral)
∠BCD = 180° − 90° = 90°
∠ADC = `1/2angleAOC`
= `1/2(180^@)`
= 90° ...(Considering AC as a chord)
∠ADC + ∠ABC = 180° ...(Cyclic quadrilateral)
90° + ∠ABC = 180°
∠ABC = 90°
Each interior angle of a cyclic quadrilateral is of 90°. Hence, it is a rectangle.
APPEARS IN
संबंधित प्रश्न
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Prove that a cyclic parallelogram is a rectangle.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
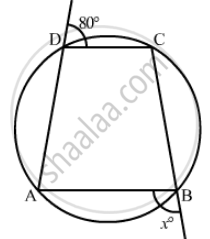
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.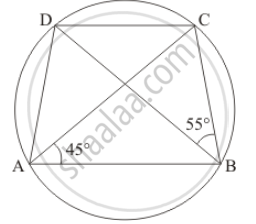
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.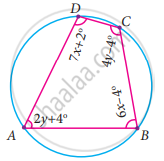
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
