Advertisements
Advertisements
प्रश्न
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
उत्तर
Given: Let ABCD be a cyclic quadrilateral and AD = BC.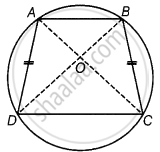
Join AC and BD.
To prove: AC = BD
Proof: In ΔAOD and ΔBOC,
∠OAD = ∠OBC and ∠ODA = ∠OCB ...[Since, same segments subtends equal angle to the circle]
AB = BC ...[Given]
ΔAOD = ΔBOC ...[By ASA congruence rule]
Adding is DOC on both sides, we get
ΔAOD + ΔDOC ≅ ΔBOC + ΔDOC
⇒ ΔADC ≅ ΔBCD
AC = BD ...[By CPCT]
APPEARS IN
संबंधित प्रश्न
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
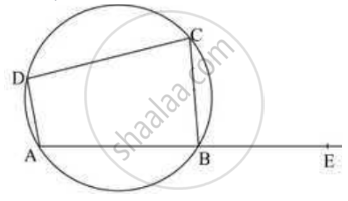
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
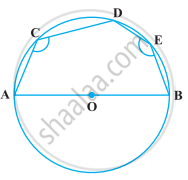
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
