Advertisements
Advertisements
Question
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
Solution
Given: Let ABCD be a cyclic quadrilateral and AD = BC.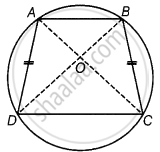
Join AC and BD.
To prove: AC = BD
Proof: In ΔAOD and ΔBOC,
∠OAD = ∠OBC and ∠ODA = ∠OCB ...[Since, same segments subtends equal angle to the circle]
AB = BC ...[Given]
ΔAOD = ΔBOC ...[By ASA congruence rule]
Adding is DOC on both sides, we get
ΔAOD + ΔDOC ≅ ΔBOC + ΔDOC
⇒ ΔADC ≅ ΔBCD
AC = BD ...[By CPCT]
APPEARS IN
RELATED QUESTIONS
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
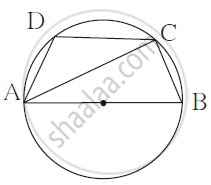
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
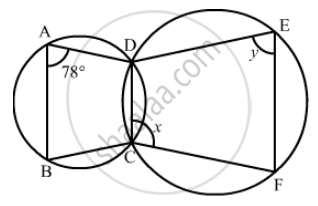
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
