Advertisements
Advertisements
Question
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
Solution
Given: ΔABC is an isosceles triangle such that AB = AC and also DE || BC.
To prove: Quadrilateral BCDE is a cyclic quadrilateral.
Construction: Draw a circle passes through the points B, C, D and E.
Proof: In ΔABC, AB = AC ...[Equal sides of an isosceles triangle]
⇒ ∠ACB = ∠ABC ...(i)
Since, DE || BC ...[Angles opposite to the equal sides are equal]
⇒ ∠ADE = ∠ACB [Corresponding angles] ...(ii)
On adding both sides by ∠EDC in equation (ii), we get
∠ADE + ∠EDC = ∠ACB + ∠EDC
⇒ 180° = ∠ACB + ∠EDC ...[∠ADE and ∠EDC from linear pair axiom]
⇒ ∠EDC + ∠ABC = 180° ...[From equation (i)]
Hence, BCDE is a cyclic quadrilateral, because sum of the opposite angles is 180°.
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
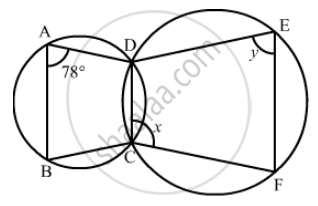
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

If non-parallel sides of a trapezium are equal, prove that it is cyclic.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
