Advertisements
Advertisements
Question
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
Solution
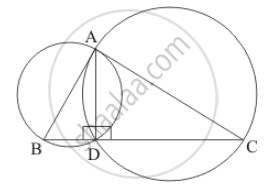
\[\angle ADB = 90° \left( \text{ Angle in a semicircle } \right)\]
\[\angle ADC = 90° \left( \text{ Angle in a semicircle } \right)\]
\[\text{ So } , \angle ADB + \angle ADC = 90° + 90° = 180\]
\[\text{ Therefore, BDC is a line } . \]
\[\text{ Hence, the point of intersection of two circles lie on the third side } .\]
APPEARS IN
RELATED QUESTIONS
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
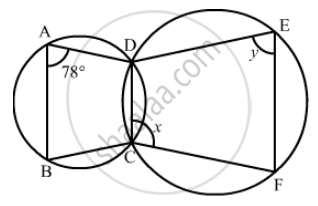
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
