Advertisements
Advertisements
Question
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution
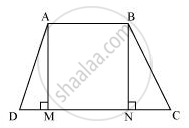
Consider a trapezium ABCD with AB | |CD and BC = AD.
Draw AM ⊥ CD and BN ⊥ CD.
In ΔAMD and ΔBNC,
AD = BC (Given)
∠AMD = ∠BNC (By construction, each is 90°)
AM = BN (Perpendicular distance between two parallel lines is same)
∴ ΔAMD ≅ ΔBNC (RHS congruence rule)
∴ ∠ADC = ∠BCD (CPCT) ... (1)
∠BAD and ∠ADC are on the same side of transversal AD.
∠BAD + ∠ADC = 180° ... (2)
∠BAD + ∠BCD = 180° [Using equation (1)]
This equation shows that the opposite angles are supplementary.
Therefore, ABCD is a cyclic quadrilateral.
APPEARS IN
RELATED QUESTIONS
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
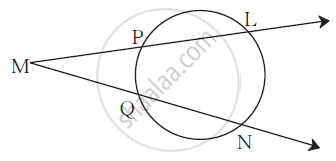
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
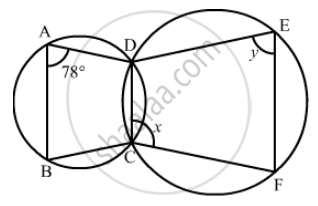
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
