Advertisements
Advertisements
प्रश्न
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
उत्तर
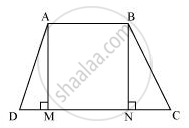
Consider a trapezium ABCD with AB | |CD and BC = AD.
Draw AM ⊥ CD and BN ⊥ CD.
In ΔAMD and ΔBNC,
AD = BC (Given)
∠AMD = ∠BNC (By construction, each is 90°)
AM = BN (Perpendicular distance between two parallel lines is same)
∴ ΔAMD ≅ ΔBNC (RHS congruence rule)
∴ ∠ADC = ∠BCD (CPCT) ... (1)
∠BAD and ∠ADC are on the same side of transversal AD.
∠BAD + ∠ADC = 180° ... (2)
∠BAD + ∠BCD = 180° [Using equation (1)]
This equation shows that the opposite angles are supplementary.
Therefore, ABCD is a cyclic quadrilateral.
APPEARS IN
संबंधित प्रश्न
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
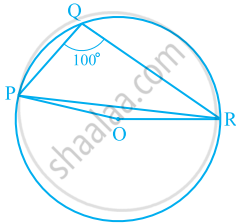
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
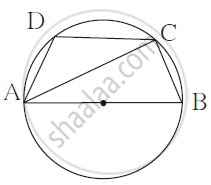
Prove that a cyclic parallelogram is a rectangle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
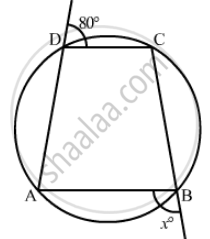
In the figure, `square`ABCD is a cyclic quadrilateral. Seg AB is a diameter. If ∠ ADC = 120˚, complete the following activity to find measure of ∠ BAC.
`square` ABCD is a cyclic quadrilateral.
∴ ∠ ADC + ∠ ABC = 180°
∴ 120˚ + ∠ ABC = 180°
∴ ∠ ABC = ______
But ∠ ACB = ______ .......(angle in semicircle)
In Δ ABC,
∠ BAC + ∠ ACB + ∠ ABC = 180°
∴ ∠BAC + ______ = 180°
∴ ∠ BAC = ______
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
