Advertisements
Advertisements
प्रश्न
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
उत्तर
Here, ABCD is a rhombus; we have to prove the four circles described on the four sides of any rhombusABCD pass through the point of intersection of its diagonals AC and BD.
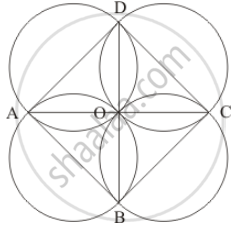
Let the diagonals AC and BD intersect at O.
We know that the diagonals of a rhombus intersect at right angle.
Therefore,
Now,
Similarly the remaining three circles with BC, CD and AD as their diameter will also pass through O.
Hence, all the circles with described on the four sides of any rhombus ABCD pass through the point of intersection of its diagonals AC and BD.
APPEARS IN
संबंधित प्रश्न
Prove that "Opposite angles of a cyclic quadrilateral are supplementary".
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.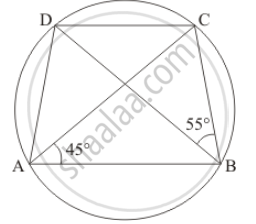
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
