Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
उत्तर
It is given that, ∠BCD = 100° and ∠ABD = 70°
As we know that sum of the opposite pair of angles of cyclic quadrilateral is 180°.
\[\angle ADC + \angle ABC = 180° \]
\[ \Rightarrow 180° - 80° + 180° - x = 180°\]
\[ \Rightarrow x = 100°\]
In ΔABD we have,
\[\angle DAB + \angle ABD + \angle BDA = 180° \]
\[ \Rightarrow \angle BDA = 180° - 150° = 30° \]
Hence, `angle ABD = 30°`
APPEARS IN
संबंधित प्रश्न
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
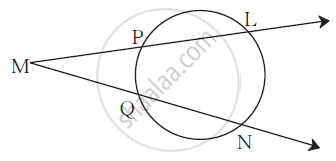
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.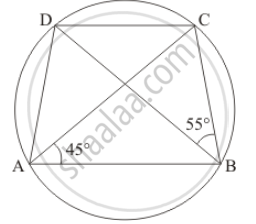
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.