Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
Solution
It is given that, ∠BCD = 100° and ∠ABD = 70°
As we know that sum of the opposite pair of angles of cyclic quadrilateral is 180°.
\[\angle ADC + \angle ABC = 180° \]
\[ \Rightarrow 180° - 80° + 180° - x = 180°\]
\[ \Rightarrow x = 100°\]
In ΔABD we have,
\[\angle DAB + \angle ABD + \angle BDA = 180° \]
\[ \Rightarrow \angle BDA = 180° - 150° = 30° \]
Hence, `angle ABD = 30°`
APPEARS IN
RELATED QUESTIONS
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
Find all the angles of the given cyclic quadrilateral ABCD in the figure.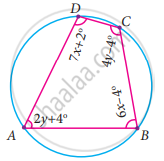
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
