Advertisements
Advertisements
Question
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution
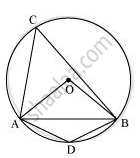
In ΔOAB,
AB = OA = OB = radius
∴ ΔOAB is an equilateral triangle.
Therefore, each interior angle of this triangle will be of 60°.
∴ ∠AOB = 60°
∠ACB = `1/2angleAOB`
∠ACB = `1/2(60^@)`
∠ACB = 30°
In cyclic quadrilateral ACBD,
∠ACB + ∠ADB = 180° ...(Opposite angle in cyclic quadrilateral)
⇒ ∠ADB = 180° − 30° = 150°
Therefore, the angles subtended by this chord at a point on the major arc and the minor arc are 30° and 150° respectively.
APPEARS IN
RELATED QUESTIONS
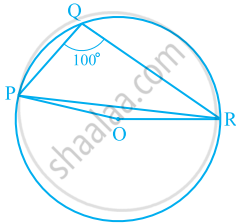
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.