Advertisements
Advertisements
Question
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
Solution
It is given that ∠A – ∠C = 60° and ABCD is a cyclic quadrilateral.
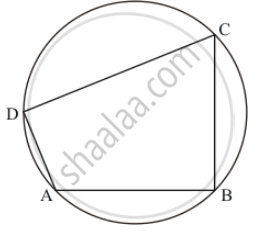
We have to prove that smaller of two is 60°
Since ABCD is a cyclic quadrilateral
So ∠A + ∠C = 180° (Sum of opposite pair of angles of cyclic quadrilateral is 180°) ..… (1)
And,
∠A – ∠C = 60° (Given) ..… (2)
Adding equation (1) and (2) we have
`2angle A = 240° `
`angle A =( 240° )/2`
= 120°
So, ∠C = 60°
Hence, smaller of two is 60°.
APPEARS IN
RELATED QUESTIONS
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
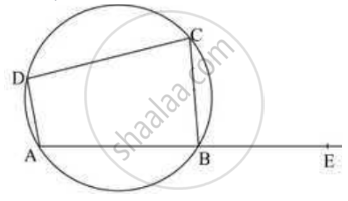
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
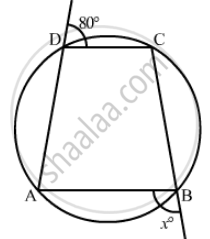
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

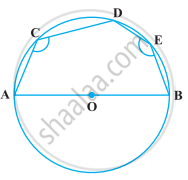
ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
In the following figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
