Advertisements
Chapters
2: Exponents of Real Numbers
3: Rationalisation
4: Algebraic Identities
5: Factorisation of Algebraic Expressions
6: Factorisation of Polynomials
7: Linear Equations in Two Variables
8: Co-ordinate Geometry
9: Introduction to Euclid’s Geometry
10: Lines and Angles
11: Triangle and its Angles
12: Congruent Triangles
13: Quadrilaterals
14: Areas of Parallelograms and Triangles
▶ 15: Circles
16: Constructions
17: Heron’s Formula
18: Surface Areas and Volume of a Cuboid and Cube
19: Surface Areas and Volume of a Circular Cylinder
20: Surface Areas and Volume of A Right Circular Cone
21: Surface Areas and Volume of a Sphere
22: Tabular Representation of Statistical Data
23: Graphical Representation of Statistical Data
24: Measures of Central Tendency
25: Probability
![RD Sharma solutions for Mathematics [English] Class 9 chapter 15 - Circles RD Sharma solutions for Mathematics [English] Class 9 chapter 15 - Circles - Shaalaa.com](/images/8193647912-mathematics-english-class-9_6:1a030933ece146238cec338f12706a07.jpg)
Advertisements
Solutions for Chapter 15: Circles
Below listed, you can find solutions for Chapter 15 of CBSE RD Sharma for Mathematics [English] Class 9.
RD Sharma solutions for Mathematics [English] Class 9 15 Circles Exercise 15.1 [Pages 5 - 6]
Fill in the blank:
All points lying inside/outside a circle are called .................. points/ .....................points.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
Fill in the blank
A continuous piece of a circle is ............... of the circle
Fill in the blank:
The longest chord of a circle is a ................of the circle.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
true or false
A circle is a plane figure.
true or false
Line segment joining the centre to any point on the circle is a radius of the circle,
true or false
If a circle is divided into three equal arcs each is a major arc.
true or false
A circle has only finite number of equal chords.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
true or false
Sector is the region between the chord and its corresponding arc.
true or false
The degree measure of an arc is the complement of the central angle containing the arc.
ture or false v
The degree measure of a semi-circle is 180°.
RD Sharma solutions for Mathematics [English] Class 9 15 Circles Exercise 15.2 [Pages 28 - 29]
The radius of a circle is 8 cm and the length of one of its chords is 12 cm. Find the distance of the chord from the centre.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle ofradius 10 cm.
Find the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
Give a method to find the centre of a given circle.
A line segment AB is of length 5 cm. Draw a circle of radius 4 cm passing through A and B. Can you draw a circle of radius 2 cm passing through A and B? Give reason in support of your answer.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
Given an arc of a circle, show how to complete the circle.
Given an arc of a circle, complete the circle.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. if the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre?
Two chords AB, CD of lengths 5 cm, 11 cm respectively of a circle are parallel. If the distance between AB and CD is 3 cm, find the radius of the circle.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Prove that two different circles cannot intersect each other at more than two points.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
RD Sharma solutions for Mathematics [English] Class 9 15 Circles Exercise 15.3 [Page 47]
Three girls Ishita, Isha and Nisha are playing a game by standing on a circle of radius 20 m drawn in a park. Ishita throws a ball o Isha, Isha to Nisha and Nisha to Ishita. If the distance between Ishita and Isha and between Isha and Nisha is 24 m each, what is the distance between Ishita and Nisha.
A circular park of radius 40 m is situated in a colony. Three boys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk
to each other.
RD Sharma solutions for Mathematics [English] Class 9 15 Circles Exercise 15.4 [Pages 72 - 74]
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

In the below fig. O is the centre of the circle. Find ∠BAC.
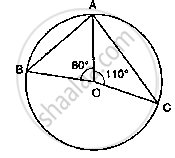
If O is the centre of the circle, find the value of x in the following figure:

If O is the centre of the circle, find the value of x in the following figure:
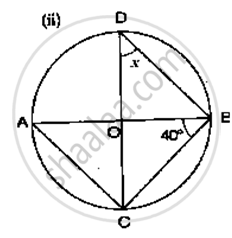
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
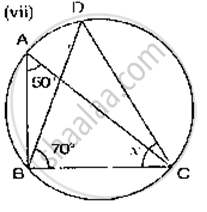
If O is the centre of the circle, find the value of x in the following figure
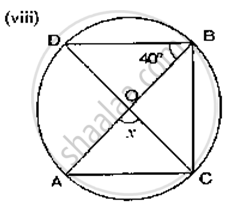
If O is the centre of the circle, find the value of x in the following figure
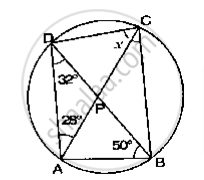
If O is the centre of the circle, find the value of x in the following figure
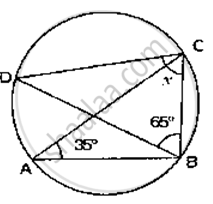
If O is the centre of the circle, find the value of x in the following figures.
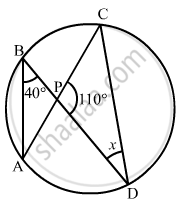
If O is the centre of the circle, find the value of x in the following figures.

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
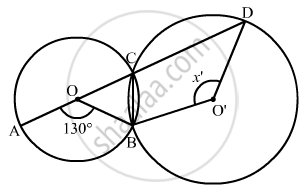
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
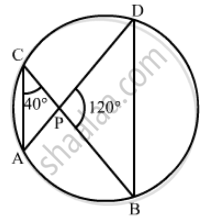
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

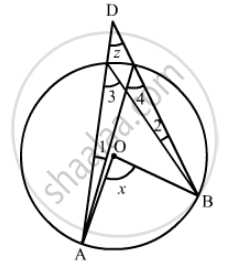
In the given figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
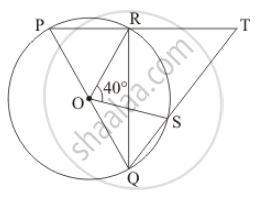
In the given figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.
RD Sharma solutions for Mathematics [English] Class 9 15 Circles Exercise 15.5 [Pages 100 - 104]
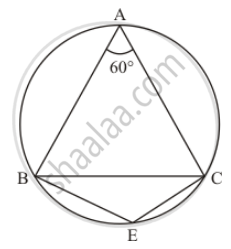
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
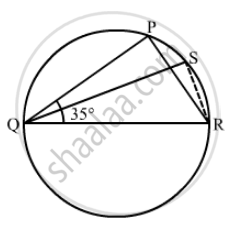
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
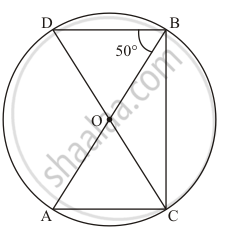
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

In the given figure, O is the centre of the circle. Find ∠CBD.

In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
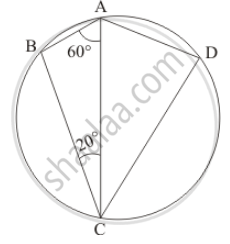
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
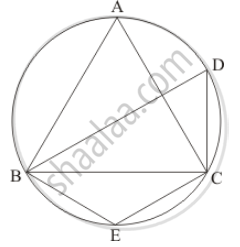
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
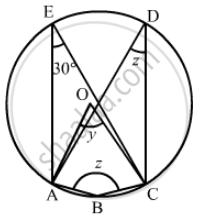
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
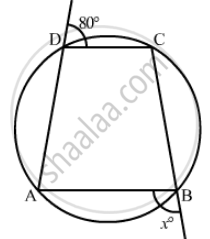
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
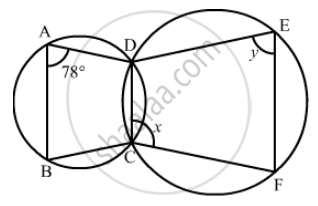
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
ABCD is a cyclic quadrilateral in ∠BCD = 100° and ∠ABD = 70° find ∠ADB.
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.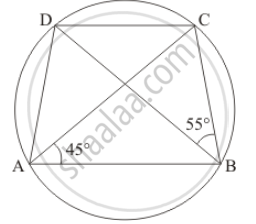
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
RD Sharma solutions for Mathematics [English] Class 9 15 Circles Exercise 15.6 [Pages 107 - 109]
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
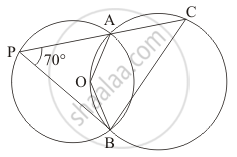
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
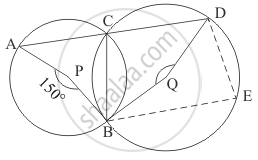
In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
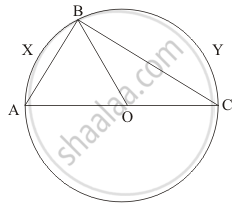
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

RD Sharma solutions for Mathematics [English] Class 9 15 Circles Exercise 15.7 [Pages 109 - 112]
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
15 cm
16 cm
17 cm
34 cm
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
- \[\sqrt{5} \] cm
- \[2\sqrt{5}\] cm
\[2\sqrt{7} \] cm
- \[\sqrt{7}\] cm
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
60°
45°
30°
15°
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
70°
100°
125°
150°
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
12 cm
12 cm
12 cm
18 cm
One chord of a circle is known to be 10 cm. The radius of this circle must be
5 cm
greater than 5 cm
greater than or equal to 5 cm
less than 5 cm
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
3 cm
4 cm
5 cm
6 cm
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
60°
90°
120°
none of these
Let C be the mid-point of an arc AB of a circle such that m \[ \stackrel\frown{AB}\] = 183°. If the region bounded by the arc ACB and the line segment AB is denoted by S, then the centre O of the circle lies
in the interior of S
in the exertior of S
on the segment AB
on AB and bisects AB
In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
90° and 270°
90° and 90°
270° and 90°
60° and 210°
If A and B are two points on a circle such that m \[ \stackrel\frown{AB}\] = 260°. A possible value for the angle subtended by arc BA at a point on the circle is
100°
75°
50°
25°
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
30°
60°
90°
120°
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
rhombus
rectangle
parallelogram
square
If ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \[\stackrel\frown{ABC}\] to the circumference is ______.
1 : 4
3 : 4
3 : 8
1 : 2
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
60°
75°
120°
150°
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
41°
23°
67°
18°
If A , B, C are three points on a circle with centre O such that ∠AOB = 90° and ∠BOC = 120°, then ∠ABC =
60°
75°
90°
135°
The greatest chord of a circle is called its
radius
secant
diameter
none of these
Angle formed in minor segment of a circle is
acute
obtuse
right angle
none of these
Number of circles that can be drawn through three non-collinear points is
1
0
2
3
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
45°
60°
75°
90°
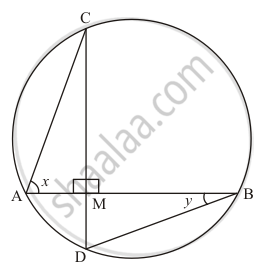
In the given figure, if ∠ABC = 45°, then ∠AOC =
45°
60°
75°
90°
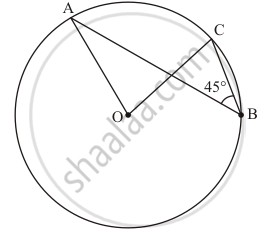
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

35°
45°
55°
65°
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
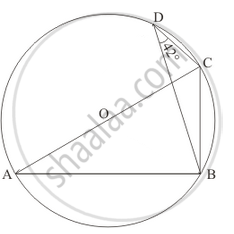
42°
48°
58°
52°
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
2AB
- \[\sqrt{2}\]
- \[\frac{1}{2}AB\]
- \[\frac{1}{\sqrt{2}}AB\]
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circle is
- \[\sqrt{r}\]
- \[\sqrt{2}r AB\]
- \[\sqrt{3}r\]
- \[\frac{\sqrt{3}}{2}\]
If AB is a chord of a circle, P and Q are the two points on the circle different from A and B, then
∠APB = ∠AQB
∠APB + ∠AQB = 180° or ∠APB = ∠AQB
∠APB + ∠AQB = 90°
∠APB + ∠AQB = 180°
AB and CD are two parallel chords of a circle with centre O such that AB = 6 cm and CD= 12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is
6 cm
- \[5\sqrt{2} cm\]
7 cm
- \[3\sqrt{5} cm\]
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is
34 cm
15 cm
23 cm
30 cm
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

130°
115°
65°
165°
Solutions for 15: Circles
![RD Sharma solutions for Mathematics [English] Class 9 chapter 15 - Circles RD Sharma solutions for Mathematics [English] Class 9 chapter 15 - Circles - Shaalaa.com](/images/8193647912-mathematics-english-class-9_6:1a030933ece146238cec338f12706a07.jpg)
RD Sharma solutions for Mathematics [English] Class 9 chapter 15 - Circles
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 9 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. RD Sharma solutions for Mathematics Mathematics [English] Class 9 CBSE 15 (Circles) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. RD Sharma textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 chapter 15 Circles are Angle Subtended by a Chord at a Point, Perpendicular from the Centre to a Chord, Equal Chords and Their Distances from the Centre, Angle Subtended by an Arc of a Circle, Concept of Circle, Cyclic Quadrilateral, Circles Passing Through One, Two, Three Points.
Using RD Sharma Mathematics [English] Class 9 solutions Circles exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in RD Sharma Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 9 students prefer RD Sharma Textbook Solutions to score more in exams.
Get the free view of Chapter 15, Circles Mathematics [English] Class 9 additional questions for Mathematics Mathematics [English] Class 9 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
