Question

If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a

Options

• rhombus

•  rectangle

• parallelogram

•  square

Answer 1

 square

The given information in the form of the following figure is as follows:

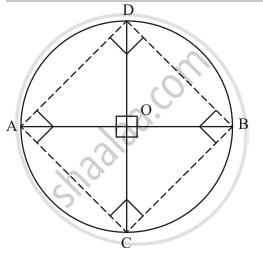
Since, four sides of the quadrilateral ACBD are four chords which subtend equal angles at the centre. Therefore,

`angleAOC = angleCOB = angleBOD = angleDOA = 90°`

    (Since AB and CD are perpendicular diameters)

So sides AC, BC, BD and AD are equal, as equal chords subtend equal angle at the centre.

So , AC = CB = BD = DA    …… (1)

We know that diameters subtend an angle of measure 90° on the circle.

So,  `angle ACB = angleCBD = angleBDA = angleDAC = 90°`  …… (2)

From (1) and (2) we can say that  `square AC BD`  is a square.