Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Theorem
Theorem: Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Consider a circle of centre O . It has PQ and RS two chords of equal length.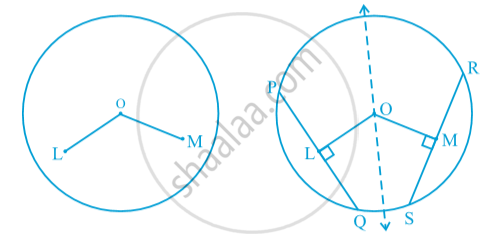
Now , draw a perpendicular from centre to PQ and RS intersecting them at L and M .
To Prove: OL = OM
Join OQ and OS.
Proof: We know that PQ =RS (given)
QL = `(PQ )/2` (perpendicular drawn from a centre to a chord bisect the chord)
Similarly, SM =`(RS)/2`
Therefore , QL = SM
Consider ∆OQL and ∆OSM
OQ = OS (radius of the same circle)
QL = SM (proved)
∠OLQ = ∠OMS = 90° (given )
∆OQL ≅ ∆OSM (SSA rule)
OL = OM (By CPCT).
Theorem: Chords equidistant from the centre of a circle are equal in length.
If you would like to contribute notes or other learning material, please submit them using the button below.
