Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Notes
Two triangles ABC and PBC on the same base BC and between the same parallels BC and AP. in following fig.
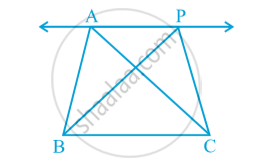
Draw CD || BA and CR || BP such that D and R lie on line AP in following fig.
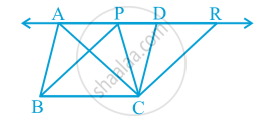
From this, you obtain two parallelograms PBCR and ABCD on the same base BC and between the same parallels BC and AR.
Therefore, ar (ABCD) = ar (PBCR)
Now ∆ ABC ≅ ∆ CDA and ∆ PBC ≅ ∆ CRP
So, ar (ABC) = `1/2` ar (ABCD) and ar (PBC) = `1/2` ar (PBCR)
Therefore, ar (ABC) = ar (PBC)
Theorem
Theorem : Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
Proof: Now, suppose ABCD is a parallelogram whose one of the diagonals is AC (see Fig.).
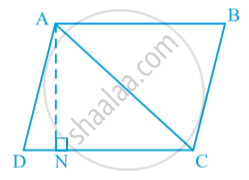
Let AN ⊥ DC. Note that
∆ ADC ≅ ∆ CBA
So, ar (ADC) = ar (CBA)
Therefore, ar (ADC) = `1/2` ar (ABCD)
=`1/2` (DC × AN)
So, area of ∆ ADC = `1/2` × base DC × corresponding altitude AN
In other words, area of a triangle is half the product of its base (or any side) and the corresponding altitude (or height).
The two triangles with same base (or equal bases) and equal areas will have equal corresponding altitudes.