Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
- Definition
- Properties of Parallel Lines
Definition
Parallel lines: Parallel lines are straight lines that never intersect and remain at a constant distance from each other. They are denoted by the symbol “∥”, meaning is parallel to.
Examples: Railroad tracks, Zebra crossings, Staircase steps
Properties of Parallel Lines
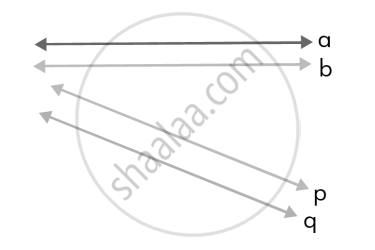
The image shows us two sets of parallel lines. Line ‘a’ is parallel to line ‘b,’ and line ‘p’ is parallel to line ‘q,’ and these parallel lines are represented as a∥b’ and 'p∥q.'
Properties of Parallel Lines:
- Parallel lines are a set of straight lines.
- Parallel lines do not intersect or cross each other.
- Parallel lines are always at the same distance from each other.
Properties of Parallel Lines Cut by a Transversal: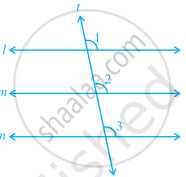
- If two parallel lines are cut by a transversal, then each pair of corresponding angles is equal in measure.
- If two parallel lines are cut by a transversal, then each pair of alternate interior angles is equal.
- If two parallel lines are cut by a transversal, then each pair of interior angles on the same side of the transversal are supplementary (sums up to 180°).
If you would like to contribute notes or other learning material, please submit them using the button below.
Video Tutorials
Shaalaa.com | Concept of Parallel Lines
to track your progress



