Topics
Number Systems
Number Systems
Algebra
Polynomials
Linear Equations in Two Variables
Algebraic Expressions
Algebraic Identities
Coordinate Geometry
Geometry
Introduction to Euclid’S Geometry
Lines and Angles
Triangles
Quadrilaterals
- Concept of Quadrilaterals - Sides, Adjacent Sides, Opposite Sides, Angle, Adjacent Angles and Opposite Angles
- Angle Sum Property of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Area
Circles
- Concept of Circle - Centre, Radius, Diameter, Arc, Sector, Chord, Segment, Semicircle, Circumference, Interior and Exterior, Concentric Circles
- Angle Subtended by a Chord at a Point
- Perpendicular from the Centre to a Chord
- Circles Passing Through One, Two, Three Points
- Equal Chords and Their Distances from the Centre
- Angle Subtended by an Arc of a Circle
- Cyclic Quadrilateral
Constructions
Mensuration
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics and Probability
Statistics
Probability
notes
The solutions of a linear equation in two variables algebraically.
Example : x +2y = 6 ...(1)
can be expressed in the form of a table as follows by writing the values of y below the corresponding values of x :
| X | 0 | 2 | 4 | 6 | ... |
| Y | 3 | 2 | 1 | 0 | ... |
Let us plot the points (0, 3), (2, 2), (4, 1) and (6, 0) on a graph paper. Now join any two of these points and obtain a line. Let us call this as line AB in following fig.
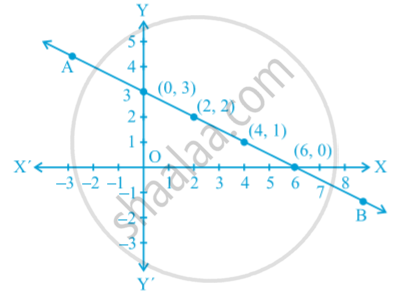
Now, pick another point on this line, say (8, –1). Pick any other point on this line AB and verify whether its coordinates satisfy the equation or not.
1. Every point whose coordinates satisfy Equation (1) lies on the line AB.
2. Every point (a, b) on the line AB gives a solution x = a, y = b of Equation (1).
3. Any point, which does not lie on the line AB, is not a solution of Equation (1).
The every point on the line satisfies the equation of the line and every solution of the equation is a point on the line. In fact, a linear equation in two variables is represented geometrically by a line whose points make up the collection of solutions of the equation. This is called the graph of the linear equation. So, to obtain the graph of a linear equation in two variables, it is enough to plot two points corresponding to two solutions and join them by a line.
Remark : The reason that a, degree one, polynomial equation ax + by + c = 0 is called a linear equation is that its geometrical representation is a straight line.
