Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Notes
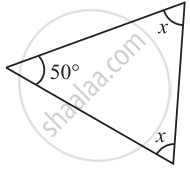
Angle Sum Property of a Triangle:
There is a remarkable property connecting the three angles of a triangle.
- Draw a triangle. Cut on the three angles. Rearrange them as shown in the following Figure. The three angles now constitute one angle. This angle is a straight angle and so has measure 180°.

Thus, the sum of the measures of the three angles of a triangle is 180°.
∴ ∠1 + ∠2 + ∠3 = 180°
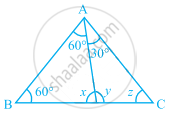
- Take a piece of paper and cut out a triangle, say, ∆ABC.
Make the altitude AM by folding ∆ABC such that it passes through A.
Fold now the three corners such that all the three vertices A, B, and C touch at M.

You find that all the three angles form together a straight angle. This again shows that the sum of the measures of the three angles of a triangle is 180°.
∴ ∠B + ∠A + ∠C = 180°
Theorem
Angle Sum Property of a Triangle:
Theorem: The sum of the angles of a triangle is 180°.
Construction: Draw a line XPY parallel to QR through the opposite vertex P.
Proof:
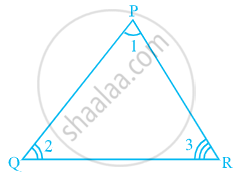
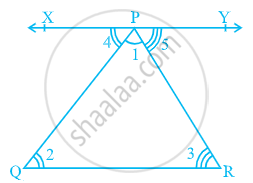
In △ PQR,
Sum of all angles of a triangle is 180°.
∠PQR + ∠PRQ + ∠QPR = 180°......(1)
Since XY is a straight line, it can be concluded that:
Therefore, ∠XPY + ∠QRP + ∠RPY = 180°.
But XPY || QR and PQ, PR are transversals.
So,
∠XPY = ∠PQR.....(Pairs of alternate angles)
∠RPY = ∠PRQ.....(Pairs of alternate angles)
Substituting ∠XPY and ∠RPY in (1), we get
∠PQR + ∠PRQ + ∠QPR = 180°
Thus, The sum of the angles of a triangle is 180°.
Example
In the given figure find m∠P.
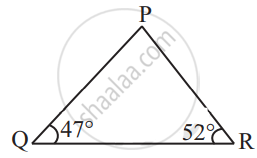
By angle sum property of a triangle,
m∠P + 47° + 52° = 180°
Therefore,
m∠P = 180° – 47° – 52°
m∠P = 180° – 99°
m∠P = 81°