Advertisements
Advertisements
Question
In the following triangle, find the value of x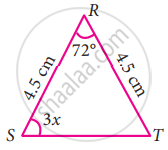
Solution
Let ∠S = 3x°
Given `bar("RS")` = Given `bar("RT")` = 4.5 cm
Given ∠S = ∠T = 3x° ...[∵ Angles opposite to equal sides are equal]
By angle sum property of a triangle we have,
∠R + ∠S + ∠T = 180°
72° + 3x + 3x = 180°
72° + 6x = 180°
x = `(108^circ)/6`
x = 18°
APPEARS IN
RELATED QUESTIONS
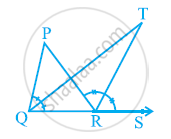
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
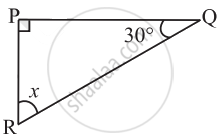
Find the value of the unknown x in the following diagram:
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
Prove that a triangle must have atleast two acute angles.
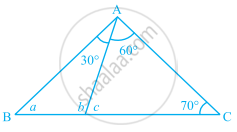
In the given figure, find the values of a, b and c.
In the given figure, find the measures of ∠PON and ∠NPO.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

