Advertisements
Advertisements
Question
In the given figure, find the measures of ∠PON and ∠NPO.
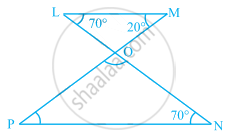
Solution
In ∆LOM,
∠LOM + ∠OLM + ∠OML = 180° ......[Angle sum property]
⇒ ∠LOM + 70° + 20° = 180°
⇒ ∠LOM = 180° – 70° – 20° = 90°
∠LOM = ∠PON ......[Vertically opposite angles]
∴ ∠PON = 90°
Now, In ΔΡΟΝ,
∠PON + ∠ONP + ∠NPO = 180° ......[Angle sum property]
⇒ 90° + 70° + ∠NPO = 180°
⇒ ∠NPO = 180° – 90° – 70° = 20°
Thus, ∠PON = 90° and ∠NPO = 20°
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown x in the following diagram:
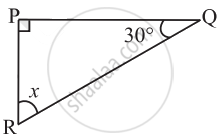
Find the value of the unknown x in the following diagram:
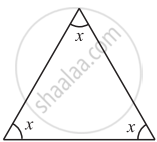
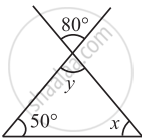
Find the value of the unknown x and y in the following diagram:
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
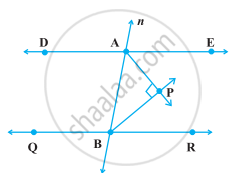
Prove that a triangle must have atleast two acute angles.
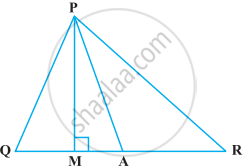
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
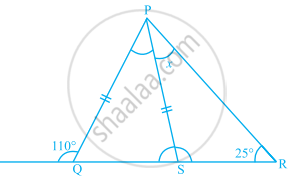
In the given figure, PQ = PS. The value of x is ______.
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
