Advertisements
Advertisements
प्रश्न
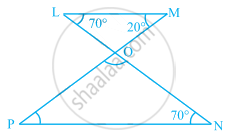
In the given figure, find the measures of ∠PON and ∠NPO.
उत्तर
In ∆LOM,
∠LOM + ∠OLM + ∠OML = 180° ......[Angle sum property]
⇒ ∠LOM + 70° + 20° = 180°
⇒ ∠LOM = 180° – 70° – 20° = 90°
∠LOM = ∠PON ......[Vertically opposite angles]
∴ ∠PON = 90°
Now, In ΔΡΟΝ,
∠PON + ∠ONP + ∠NPO = 180° ......[Angle sum property]
⇒ 90° + 70° + ∠NPO = 180°
⇒ ∠NPO = 180° – 90° – 70° = 20°
Thus, ∠PON = 90° and ∠NPO = 20°
APPEARS IN
संबंधित प्रश्न
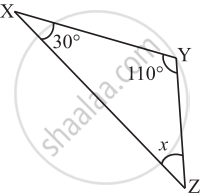
Find the value of the unknown x in the given diagram:
In the following triangle, find the value of x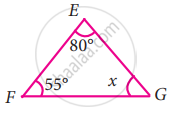
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
By which of the following criterion two triangles cannot be proved congruent?
The sum of the measures of three angles of a triangle is greater than 180°.
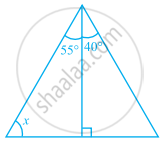
In the given figure, find the value of x.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

